|
Listing 1:
// Beispiel mit allen Elementen des
Editors
// faktor: Zoomfaktor für Editor, Muliplikator für Parameter
// defaultwerte:
faktor 1.0,1.0
// verschieben: x,y,z
// Verschieben aller nachfolgender Elemente um die angegebenen Werte
verschieben 0,80,0
// alle Angaben in mm
//Erdgeschoß
// color: Rotanteil [0...1], Grünanteil [0...1], Blauanteil [0...1],
Geländefarbe
color 1.00,1.00,0.50 // helles gelb
// box: 1.Punkt x1,y1,z1, gegenüberliegender Punkt x2,y2,z2
box -50,-30,0,50,30,50
// Dach
// texture: Nummer, Größe, Farbmischung, Drehwinkel
texture 20,3,0,0
// hexaeder: Körper mit 6 ebenen Flächen
// definiert durch 8 Punkte im Raum, deren Reihenfolge wichtig ist.
(sonst stimmen die Farben nicht !)
// Punkte 1-4: unten: beginnend mit links vorne, rechts vorne, rechts
hinten, links hinten,
// Punkte 5-8: oben: ....
hexaeder -55,-35,50, 55,-35,50, 55,35,50, -55,35,50, -30,-20,80,
30,-20,80, 30,20,80, -30,20,80
texture 0
// Turmaufbau
color 0.75,0.75,0.75 // grau
// pyramide: Mittelpunkt x,y,z, Hoehe, Seitenlänge unten/oben
pyramide 10,0,80, 40,30,30
// Dach vom Turm
color 1,0,0 //rot
pyramide 10,0,120, 40,35,0
// Fahnenstange auf Dach
color 0.50,0.50,1.00 // blau
// cylinder: Mittelpunkt x,y,z, Hoehe, Radius unten, Radius oben,Anzahl
Seiten; 8-10: Drehwinkel um x,y,z-Achse
cylinder -25,0,80, 100,1,1,8, 0,0,0
// Text
//text: x,y,z,Drehwinkel um x,y,z-Achse,Breite,Höhe,Text
text 0,-50,0, 0,0,0,200,20,WinTrack-Editor
// Fahne
// streifen: x1,y1,z1,x2,y2,z2,x3,y3,z3,.... x8,y8,z8
// das sind nebeneinander liegende Streifen, Punktanzahl min. 3, max. 8
!
// Punkt 7 *------------------* Punkt 8
// |
|
// Punkt 5 *------------------* Punkt 6
// |
|
// Punkt 3 *------------------* Punkt 4
// |
|
// Punkt 1 *------------------* Punkt 2
color 0.00,1.00,0.00 // gruen
streifen -25,0,160, -25,0,180, -55,0,160, -55,0,180, -75,10,160,
-75,10,180
// Kugel auf Fahnenstange
// kugel: Mittelpunkt x,y,z, radius, genauigkeit
// zu genauigkeit: je nach Größe und gewünschter Genauigkeit sollten
hier Werte zwischen 3 und 32 verwendet werden.
// Werte größer als 32 werden auf 32 reduziert.
kugel -25,0,182, 3,8
// Geländer auf Dach
color 0.00,0.00,1.00 // blau
// Daten automatisch erzeugt mit Menü Einfügen | Geländer !!!!
// Geländer: -28.00,-18.00,80.00, -28.00,18.00,80.00,
15.00,5,2,1.00
box -28.50,-18.50,80.00, -27.50,-17.50,95.00
box -28.50,-9.50,80.00, -27.50,-8.50,95.00
box -28.50,-0.50,80.00, -27.50,0.50,95.00
box -28.50,8.50,80.00, -27.50,9.50,95.00
box -28.50,17.50,80.00, -27.50,18.50,95.00
cylinder -28.00,-18.00,87.50, 36.00,0.50,0.50,4.00, 0.00,90.00,90.01
cylinder -28.00,-18.00,95.00, 36.00,0.50,0.50,4.00, 0.00,90.00,90.01
// 2D-Elemente für die Anzeige bei der Wintrack-Planung
color 0.7,0,0
//rechteck2d: 1.Punkt x,y, gegenüberliegender Punkt x,y, Ausfüllen?
// Reihenfolge bei übereinanderliegenden Fläschen ist wichtig ! Aufbau
von unten nach oben !
rechteck2d -55,-35, 55,35,1
rechteck2d -30,-20, 30,20,0
// linie2d: 1.Punkt x,y, 2.Punkt x,y
linie2d -55,-35, -30,-20
linie2d -55,35, -30,20
linie2d 55,-35, 30,-20
linie2d 55,35, 30,20
// kreis2d: Mittelpunkt x,y, Radius, Ausfuellen ?
color 0,1,0
kreis2d -25,0,5,1
//anfasser2d: Position des Anfasserrechtecks x,y
anfasser2d -30,0
// weiteres Element (für Beispiel nicht benötigt)
// polygon: x1,y1,z1,x2,y2,z2,x3,y3,z3,.... x8,y8,z8
// das ist eine Polygon-Fläche, Punktanzahl min. 3, max. 8 !
// die Reihenfolge der Punkte muß bei Blick auf die sichtbare Seite im
Gegenuhrzeigersinn erfolgen.
// Anderenfalls ist der Farbton dunkler.
// wichtig: nur konvexe Polygone werden immer richtig gezeichnet. Siehe
dazu auch Wintrack Handbuch S.40.
//polygon 30,-30,0, 0,-30,0, 0,-60,0, 15,-80,0, 30,-60,0
|
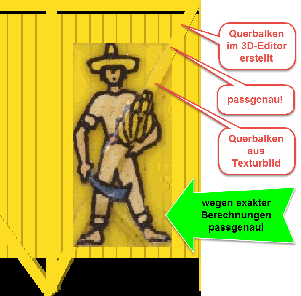
 Abb.1
Abb.1 Abb.2
Abb.2 Abb.3
Abb.3

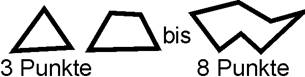
 (Quader)
(Quader)

 bis
bis
 (Kegel)
(Kegel) (ab Wintrack
Version 12)
(ab Wintrack
Version 12)
 (ab Wintrack
Version 12)
(ab Wintrack
Version 12)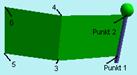
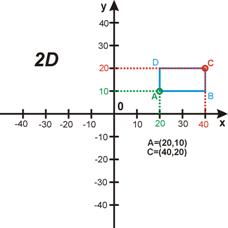 Abb.4
Abb.4 Abb.5
Abb.5 Abb.6
Abb.6














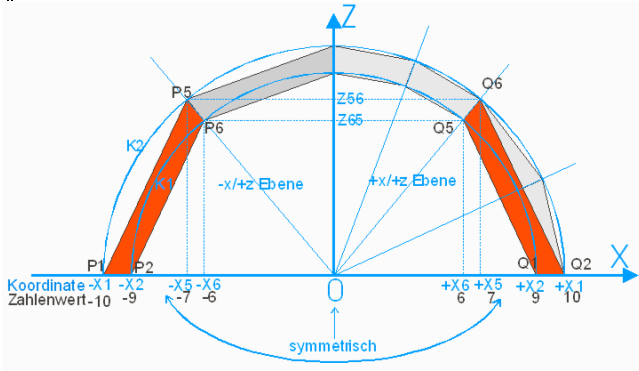

 Abb18
Abb18 Abb.19
Abb.19 Abb.20
Abb.20



 Abb.24
Abb.24 Abb. 25
Abb. 25 Abb. 26
Abb. 26 Abb. 27
Abb. 27
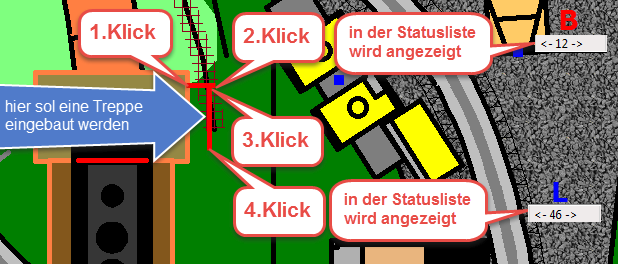

 Abb.32
Abb.32
 Abb.34
3D-Ansicht von TEdit-3D
Abb.34
3D-Ansicht von TEdit-3D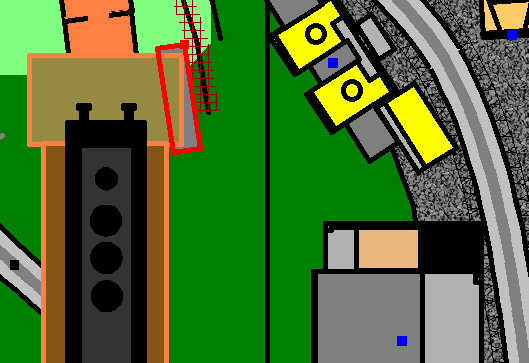

 Abb.37
Abb.37 Abb.38
Abb.38